A Review
Roughly speaking, a spectral sequence is a system for keeping tracking of collections of exact sequences with maps between them.
Recall the Snake Lemma : given \(A,B,C\) chain complexes fitting into a short exact sequence \begin{align*} 0 \xrightarrow{} A \xrightarrow{i} B \xrightarrow{p} C \xrightarrow{} 0\end{align*}
there is a canonical long exact sequence in homology \begin{align*} \cdots \xrightarrow{} H_n(A) \xrightarrow{i_*} H_n(B) \xrightarrow{p_*} H_n(C) \xrightarrow{\delta} H_{n-1}(A) \xrightarrow{} \cdots\end{align*}
where \(\delta\) is the “connecting homomorphism”.
Now specialize to the case where \(A_*\) is a chain complex, \(B_* \subset A_*\) is a subcomplex, and consider the quotient \(A_*/B_*\). We have a short exact sequence \begin{align*} 0 \xrightarrow{} B_* \xrightarrow{i} A_* \xrightarrow{p} A_*/B_* \xrightarrow{} 0\end{align*}
Applying the snake lemma yields the long exact sequence in homology
\begin{align*}\dots \xrightarrow{} H_n(B_*) \xrightarrow{i_*} H_n(A_*) \xrightarrow{p_*} H_n(A_*/B_*) \xrightarrow{\delta} H_{n-1}(B_*) \xrightarrow{} \cdots\end{align*}
where \(\delta\) is defined in the following way:
Given an arbitrary class \(\alpha \in H_n(A_*/B_*)\), pick a representative \(x \in A_*\) so that \(\alpha = [x]\). Since \({\partial}x \in B_*\), we can define \({\partial}(\alpha) = {\partial}([x]) \coloneqq[{\partial}x] \in H_{n-1}(B)\).
Supposing that the computation of the homologies for the subcomplex \(B_*\) and the quotient complex \(A_*/B_*\) are tractable, we can break this long exact sequence up into a collection of short exact sequences \begin{align*} 0 \xrightarrow{} \operatorname{coker}\delta \xrightarrow{} H_i(A_*) \xrightarrow{} \ker \delta \xrightarrow{} 0 \end{align*}
This yields the following procedure for computing \(H_i(A_*)\):
- Compute \(H_i(B_*)\) and \(H_i(A_*/B_*)\)
-
Look at the two term chain complex \(H_i(A_*/B_*) \xrightarrow{\delta} H_{i-1}(B_*)\)
- Take its homology, yielding \(G_1H_i\) and \(G_2H_i\)
- Solve the extension problem for the short exact sequence \(0 \xrightarrow{} G_0H_i \xrightarrow{} H_i(A_*) \xrightarrow{}G_1H_i \xrightarrow{} 0\)
Filtrations
A filtered \(R\)-module is an \(R\)-module \(A\) with a sequence of submodules \(\left\{{A_i}\right\}_{i\in {\mathbf{Z}}}\) such that \(A_i \subset A_{i+1}\) and \(\cup_{\mathbf{Z}}A_i = A\). Due to onerous index juggling, we write \(A_i = F_i A\).
A good example of this is a CW-complex \(X\), where \(F_iX\) is the \(i\)-skeleton of \(X\).
Given such a filtration, we can define an associated graded module \(B\) where \(B_i = A_{i}/ A_{i-1}\). This can yield a short exact sequence \(0 \xrightarrow{} A_{i-1} \xrightarrow{} A_i \xrightarrow{} B_i \xrightarrow{} 0\)
A filtered chain complex is a chain complex \((C_*, {\partial})\) along with a filtration on each \(n\)-chain, \(\left\{{F_iC_n}\right\}_{i\in{\mathbf{Z}}}\), such that \({\partial}(F_i C_n) \subseteq F_iC_{n-1}\) (i.e. the differential preserves the filtration).
Possible example: Compute Serre spectral sequences with \({ \mathbf{F} }_p\) coefficients.
Example
The most basic example is a spectral sequence is \(E^r_{p,q}\), where \(r\) denotes the page of the spectral sequence and the \(E_{p,q}\) is a bigraded collection of abelian groups. Furthermore, we can take a “first quadrant” sequence, where only the \(p>0, q>0\) terms are nontrivial. The differentials are then defined on any given page as a “shift map” that translates \(p+r\) horizontal indices and \(q-(r-1)\) vertical indices (direction depends on indexing vs. “coindexing”). Here is an example of an \(r=2\) page:
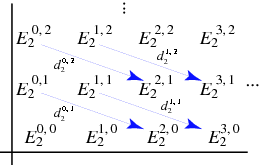
In this case, \(\lim_{r\rightarrow \infty} E^r_{p,q}\) stabilizes for any given \((p,q)\) term, so we define it as \(E^\infty_{p,q}\).
Common Types
-
Serre
- Cohomology groups of spaces in a fibration
-
Leray-Serre
- “Cohomology” of complexes of sheaves
- Special case of Grothendieck
-
Grothendieck
- The resulting derived functor from a composition of two known derived functors
-
Adams
- Higher homotopy groups of spheres